Как найти квадратный корень по методу евклида. Алгоритм евклида - нахождение наибольшего общего делителя. Индо-арабская система счисления

1ЛЕКЦИЯ 2 ВЫЧИСЛЕНИЕ НАИБОЛЬШЕГО ОБЩЕГО ДЕЛИТЕЛЯ Алгоритм Евклида При работе с большими составными числами их разложение на простые множители, как правило, неизвестно. Но для многих прикладных задач теории чисел поиск разложения числа на множители является важной, часто встречающейся практической задачей. В теории чисел существует сравнительно быстрый способ вычисления НОД двух чисел, который называется алгоритмом Евклида. Алгоритм 1. Алгоритм Евклида . Вход. Целые числа а, b- 0 < b < а. Выход. d = НОД (a,b). 1. Положить r 0 a, r 1 b, i Найти остаток r i+1 от деления r i 1 на r i. 3. Если r i+1 = 0, то положить d r i. В противном случае положить i i + 1 и вернуться на шаг Результат: d. Теорема. Для любых а, b > 0 алгоритм Евклида останавливается и выдаваемое им число d является наибольшим общим делителем чисел а и b. Доказательство . По теореме о делении с остатком для любого i 1 имеем r i 1 = q i r i + r i+1, где 0 r i+1 < r i. Получаем монотонно убывающую последовательность неотрицательных целых чисел r 1 > r 2 > r 3 >... 0, ограниченную снизу. Такая последовательность не может быть бесконечной, следовательно, алгоритм Евклида останавливается. Бинарный алгоритм Евклида Бинарный алгоритм Евклида вычисления НОД оказывается более быстрым при реализации этого
2алгоритма на компьютере, поскольку использует двоичное представление чисел а и b. Бинарный алгоритм Евклида основан на следующих свойствах наибольшего общего делителя (считаем, что 0 < b а): 1) если оба числа а и b четные, то НОД(a,b) = 2 НОД(a/2, b/2) 2) если число а нечетное, число b четное, то НОД(a, b) = НОД(а, b/2)- 3) если оба числа а и b нечетные, а > b, то НОД(а, b) = НОД(а b, b)- 4) если а = b, то НОД(а, b) = а. Алгоритм 2. Бинарный алгоритм Евклида . Вход. Целые числа a, b- 0 < b а. Выход. d = HOД(a,b). 1. Положить g Пока оба числа а и b четные, выполнять а a/2, b b/2, g 2g до получения хотя бы одного нечетного значения а или b. 3. Положить u a, v b. 4. Пока u 0, выполнять следующие действия Пока u четное, полагать u u/ Пока v четное, полагать v v/ При u v положить u u v. В противном случае положить v v u. 5. Положить d gv. 6. Результат: d. Расширенный алгоритм Евклида Расширенный алгоритм Евклида находит наибольший общий делитель d чисел а и b и его линейное представление, т. е. целые числа x и у, для которых ах + by = d, и не требует «возврата», как в рассмотренном примере. Пусть d НОД для a и b, т. е. d = (a, b), где a > b. Тогда существуют такие целые числа x и y, что d = ax + by. Иными словам, НОД двух чисел можно представить в
3виде линейной комбинации этих чисел с целыми коэффициентами. Алгоритм 3. Схема расширенного алгоритма Евклида. 1. Определить = 1, = 0, = 0, = 1, α = a, β = b. 2. Пусть число q частное от деления числа a на число b, а число r остаток от деления этих чисел (т. е. a = qb + r). a = b- b = r- t = - //t = x i-1 - = t q- // = x i для правой части = x i+1 для правой- //t = y i-1 - = t q- 5. Возвращаемся на шаг Определяем x = x 0, y = y 0, d = αx + βy. Вариант расширенного алгоритма Евклида Вход. Целые числа а, b- 0 < b а. Выход: d = НОД(а, b)- такие целые числа х, у, что ах + by = d. 1. Положить r 0 а, r 1 b, х 0 1, x 1 0, у 0 0, y 1 1, i 1 2. Разделить с остатком r i 1 на r i,: r i 1 = q i r i +r i Если r i+1 = 0, то положить d r i, х x i у y i. В противном случае положить x i+1 x i 1 x i, y i+1 y i 1 y i, i i + 1 и вернуться на шаг Результат: d, х, у. Корректность определения чисел х и у,
4вычисляемых алгоритмом, показывает следующая теорема. Теорема 4. На каждой итерации алгоритма 3 выполняется равенство аx i + by i = r i, при i 0. Доказательство . Воспользуемся методом математической индукции. Для i = 0 и i = 1 требуемое равенство имеет место в силу шага 1 алгоритма 3. Допустим, что оно справедливо для i 1 и для i. Тогда на шаге 3 получаем x i+1 = x i 1 x i и y i+1 = y i 1 y i. Следовательно, аx i+1 + by i+1 = a(x i 1 x i) + b(y i 1 y i,) = ax i 1 + by i 1 (ax i + by i) = r i 1 r i = r i+1. Пример. Дано a = 1769, b = 551. Используя расширенный алгоритм Эвклида, найти целые числа x и y такие, что d = ax + by, где d НОД чисел a и b. I этап последовательности вычислений. 1. Определить = 1, = 0, = 0, = 1, α = 1769, β = Частное от деления q = a/b = 1769/551 = 3, а остаток от деления r = 116. a = 551- b = 116- t = =0: = t q = 1 0 = 1 = 0- = t q = 3- следующие промежуточные значения
5параметров: a= 551, b = 116, = 0, = 1, = 1, = Так как остаток от деления r 0, то возвращаемся на шаг 2. II этап последовательности вычислений. 1. Значение параметров: a = 551, b = 116, = 0, = 1, = 1, = Частное от деления q = a/b = 551/116 = 4, а остаток от деления r = 87. a = 116- b = 87- t = = 0- =1: = t q = = 4 = 3- = t q = 1 (3) 4 = 13- следующие промежуточные значения параметров: a= 116, b = 87, = 1, = 4, = 3, = Так как остаток от деления r 0, то возвращаемся на шаг 2. III этап последовательности вычислений. 1. Значение параметров: a= 116, b = 87, = 1, = 4, = 3, = Частное от деления q = a/b = 116/87 = 1, а остаток от деления r = 29.
6a = 87- b = 29- t = = 4: = t q = 1 (4) 1 = 5- = 3- = 13- = t q = 3 (13) 1 = 16- следующие промежуточные значения параметров: a= 87, b = 29, = 4, = 5, = 13, = Так как остаток от деления r 0, то возвращаемся на шаг 2. IV этап последовательности вычислений. 1. Значение параметров: a= 87, b = 29, = 4, = 5, = 13, = Частное от деления q = a/b = 87/29 = 3, а остаток от деления r = 0. a = 87- b = 29- t = = 4- = 5- = 19- = 13- = 16- = t q = 13 (16) 3 = 61- следующие промежуточные значения параметров: a= 87, b = 29, = 5, = 19, = 16, = Так как остаток от деления r = 0, то выполняем шаг 6.
76. Вычисляем НОД по формуле d = αx + βy, где x = x 0 = 5, y = y 0 = 16, α= 1769, β = 551. Подставляя значение параметров, получаем d = αx + βy = = = 29. Расширенный алгоритм Евклида можно реализовать и в двоичном виде. Алгоритм 4. Расширенный бинарный алгоритм Евклида . Вход. Целые числа а, b- 0 < b а. Выход. d = НОД(a, b)- такие целые числа х, у, что ах + by = d. 1. Положить g Пока оба числа а и b четные, выполнять а a/2, b b/2, g 2g до получения хотя бы одного нечетного значения а или b. 3. Положить u a, v b, А 1, В 0, С 0, D Пока u 0, выполнять следующие действия Пока u четное, положить u u/ Если оба числа А и B четные, то положить A A/2, B B/2. В противном случае положить A (A+b)/2, B (B a)/ Пока v четное: Положить v v/ Если оба числа С и D четные, то положить С C/2, D D/2. В противном случае положить C (C + b)/2, D (D a)/ При u v положить u u v, А А С, В В D. В противном случае положить v v u, C C A, D D B. 5. Положить d gv, x С, у D. 6. Результат: d, х, у.
 

 

 
Решение уравнений в целых числах Линейные уравнения. Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.

 

Занятие 7 Число d называется наибольшим общим делителем (НОД) чисел a и b, если (1) d a и d b, а также (2) для всех x из x a и x b следует x d. В этом случае пишем d = (a, b). Лемма 1. Для любых чисел

 

Тема. Основы элементарной теории чисел и приложения- Теоретический материал. Множество вычетов по модулю, свойства сравнений. Пусть натуральное число, большее. Через Z обозначаем множество всех классов

 

Югорский физико-математический лицей ВП Чуваков ОСНОВЫ ТЕОРИИ ЧИСЕЛ Конспект лекций (0)(mod) (0)(mod) Натуральные числа N, - множество натуральных чисел, используемых для счета или перечисления

 

Глава 2 Целые, рациональные и вещественные числа 2.. Целые числа Числа, 2, 3,... называются натуральными. Множество всех натуральных чисел обозначается N, т.е. N = {,2,3,...}. Числа..., 3, 2,0,2,3,...

 

Цепные дроби Конечные цепные дроби Определение Выражение вида a 0 + a + a + + a m где a 0 Z a a m N a m N/{} называется цепной дробью а m - длиной цепной дроби a 0 a a m будем называть коэффициентами цепной

 

ЛЕКЦИЯ 1 НЕКОТОРЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ В пособии не излагается теория чисел а дан минимальный инструментарий из этой теории который в дальнейшем потребуется для изучения криптографических систем используемых

 

Горбачев НЕ Многочлены от одной переменной Решение уравнений степени Понятие многочлена Арифметические операции над многочленами Опр Многочленом (полиномом) -й степени относительно переменной величины

 

Делимость целых чисел Число а делится на число b (или b делит а) если существует такое число с, что а=bc При этом число c называется частным от деления а на b Обозначения: a - а делится на b или ba b делит

 

ЛЕКЦИЯ 12 СРВНЕНИЯ ВТОРОЙ СТЕПЕНИ ПО ПРОСТОМУ МОДУЛЮ И КВАДРАТИЧНЫЕ ВЫЧЕТЫ Общий вид сравнения второй степени по простому модулю р имеет вид (1) с 0 х 2 + с 1 х + с 2 0 mod p. Поиск решения сравнения (1)

 

Указания, решения, ответы УРАВНЕНИЯ В ЦЕЛЫХ ЧИСЛАХ. Уравнение с одной неизвестной.. Решение. Подставим в уравнение. Получим равенство (4a b 4) (a b 8) 0. Равенство A B 0, где А и В целые, выполняется,

 

Алгебраические многочлены. 1 Алгебраические многочлены степени n над полем K Определение 1.1 Многочленом степени n, n N {0}, от переменной z над числовым полем K называется выражение вида: fz = a n z n

 

Лекция Квадратичные вычеты и невычеты Лектор: НЮ Золотых Записал: Е Замараева?? сентября 00 Содержание Квадратичные вычеты и невычеты Символ Лежандра Свойства символа Лежандра Квадратичный закон взаимности

 

ГОУ Школа-интернат "Интеллектуал" И с с л е д о в а т е л ь с к а я р а б о т а п о м а т е м а т и к е на тему: «О представимости натуральных чисел в виде линейной комбинации с целыми коэффициентами»

 

Математический анализ Раздел: Неопределенный интеграл Тема: Интегрирование рациональных дробей Лектор Пахомова Е.Г. 0 г. 5. Интегрирование рациональных дробей ОПРЕДЕЛЕНИЕ. Рациональной дробью называется

 

4 Теория чисел 4 Целые числа 7 Определение Пусть, b Z Тогда делит b, если существует целое число такое что b (обозначается b) 73 Теорема (деление с остатком) Если, b Z и b, тогда найдутся такие целые

 

Математический анализ Раздел: Неопределенный интеграл Тема: Интегрирование рациональных дробей Лектор Рожкова С.В. 0 г. 5. Интегрирование рациональных дробей ОПРЕДЕЛЕНИЕ. Рациональной дробью называется

 

009-00 уч. год. 6, 9 кл. Математика. Элементы теории чисел. 4. Вычисление наибольшего общего делителя и наименьшего общего кратного Сохраним обозначения из параграфа. Для натурального числа n запись n

 

ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа). I 1 / 67 Часть I Конечные поля (поля Галуа). I ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа). I 2 / 67 Поля вычетов по модулю простого

 

5 Решение уравнений в целых числах В решении даже таких простейших уравнений, как линейное уравнение с одним неизвестным, есть свои особенности, если коэффициенты уравнения являются целыми числами, и требуется

 

Лабораторная работа 8 Вычисление наибольшего общего делителя для двух чисел при помощи алгоритма Евклида Цель работы используя алгоритм Эвклида создать программу, которая для чисел a и b определяет наибольший

 

Раздел 1. Математические основы криптографии 1 Определение поля Конечным полем GF q (или полем Галуа) называют конечное произвольное множество элементов с заданными между ними операциями сложения, умножения

 

XIX Межрегиональная олимпиада школьников по математике и криптографии Задачи для 11 класса Решение задачи 1 Сначала заметим, что если N = pq, где p и q простые числа, то количество натуральных чисел, меньших

 

Многочлены и их корни 2018 г. Гущина Елена Николаевна Определение: Многочленом степени n n N называется всякое выражение вида: P & z = a & z & + a &+, z &+, + + a, z + a., где a &, a &+, a, a. R, a &

 

Лекция 4. СТАНДАРТ AES. АЛГОРИТМ RIJNDAEL. Стандарт AES (Advnced Encrypton Stndrd) представляет собой новый стандарт шифрования с одним ключом, который заменил стандарт DES. Алгоритм Rjndel (рейн-дал)

 

Многочлены и их корни Определение: Многочленом степени n (n N) называется всякое выражение вида: P n (z) = a n z n + a n 1 z n 1 + + a 1 z + a 0, где a n, a n 1, a 1, a 0 R, a n старший коэффициент, a

 

1 Алгоритм Евклида и его сложность Определение 1. Общим делителем чисел a и b называется такое число c, что c a и c b. Определение 2. Наибольшим общим делителем чисел a и b называется такой их общий делитель,

 

ЛЕКЦИЯ 14 Вычисление квадратных корней по составному модулю Из приведенной выше теории следует, что если =, где и простые числа, группа Z изоморфна пространству Z Z. Поскольку изоморфизм сохраняет свойства

 

ЛЕКЦИЯ 3 ВЫЧИСЛЕНИЕ КВАДРАТНЫХ КОРНЕЙ ПО МОДУЛЮ Случай простого модуля Рассмотрим сравнение х a mod р, () где число р простое и целое число а не делится на p Вычисление решения x данного уравнения является

 

Программа коллоквиума по дискретной математике (основной поток) В начале коллоквиума Вы получите билет, в котором будет три вопроса: вопрос на знание определений, задача, вопрос на знание доказательств.

 

Алгоритм Шора Ю. Лифшиц. 1 декабря 005 г. План лекции 1. Подготовка (a) Разложение чисел на множители (b) Квантовые вычисления (c) Эмуляция классических вычислений. Алгоритм Саймона (a) Квантовый параллелизм

 

Из истории математики Первой достаточно объемной книгой, в которой арифметика излагалась независимо от геометрии, было Введение в арифметику Никомаха (ок нэ) В истории арифметики её роль сравнима с ролью

 

Краткое введение в начала элементарной теории чисел Денис Кириенко Летняя компьютерная школа, 1 января 2009 года Целочисленное деление Пусть дано два целых числа a и b, b 0. Целочисленным частным от деления

 

Тема 1-9: Многочлены. Построение кольца многочленов. Теория делимости. Производная А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной

 

Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0, коэффициентами

 

Лекция 6 Элементы теории чисел 1 Задача. Продолжите числовой ряд 1, 3, 5, 7, 1, 3, 5, 7, 11 1, 11, 101, 1001, 1, 11, 101, 1001, 1011, 2 Арифметика целых чисел Использует целые числа: Z = {, -2, -1, 0,

 

Многочлены Многочленом с одной переменной х степени n называют выражение вида, где - любые числа, называемые коэффициентами многочлена, причем называют старшим коэффициентом многочлена Если вместо переменной

 

1 2 Содержание. 1. Введение. 4-6 1.1. Аннотация...4 1.2. Проблема 4 1.3. Цель работы 5 1.4. Гипотеза..5 1.5. Предмет исследования... 5 1.6. Объект исследования. 5 1.7. Новизна... 5-6 1.8. Методы исследования...6

 

8.3, 8.4.2 класс, Математика (учебник Макарычев) 2018-2019 уч.год Тема модуля «Целые числа. Делимость чисел. Степень с целым показателем» В тесте проверяются теоретическая и практическая части. ТЕМА Знать

 

Лекция ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ Рациональные дроби Интегрирование простейших рациональных дробей Разложение рациональной дроби на простейшие дроби Интегрирование рациональных дробей Рациональные

 

Www.cryptolymp.ru XIX Межрегиональная олимпиада школьников по математике и криптографии (11 класс) Решение задачи 1 Сначала заметим, что если N pq, где p и q простые числа, то количество натуральных чисел,

 

Глава Целые числа Теория делимости Целыми называются числа, -3, -, -, 0, 3, те натуральные числа, 3, 4, а также нуль и отрицательные числа -, -, -3, -4, Множество всех целых чисел обозначается через

 

Министерство образования и науки РФ Уральский государственный экономический университет Ю. Б. Мельников Многочлены Раздел электронного учебника для сопровождения лекции Изд. 4-е, испр. и доп. e-mail:,

 

{тригонометрический ряд тригонометрическая система примеры - разложение на интервале [ -l- l ] для функций произвольного периода - неполные ряды разложение по синусам и косинусам четные и нечетные продолжения}

 

Теоретическая информатика II Лекция 5. Целочисленные алгоритмы: расширенный алгоритм Евклида, обратный элемент по модулю, возведение в степень по модулю. Криптография с открытым ключом, протокол RSA. Вероятностная

 

5. Коды Боуза-Чоудхури-Хоквингема Корректирующие свойства циклических кодов могут быть определены на основе двух теорем . Теорема 1. Для любых m и t существует циклический код длиной n = 2 m 1, с кратностью

 

МОДУЛЬНАЯ АРИФМЕТИКА В некоторых приложениях удобно выполнять арифметические операции над целыми числами, заданными в так называемом модульном представлении Это представление предполагает, что целое число

 

МАТЕМАТИКА ЕГЭ 00 Корянов А.Г. Задания С г. Брянск Замечания и пожелания направляйте по адресу: УРАВНЕНИЯ И НЕРАВЕНСТВА В ЦЕЛЫХ ЧИСЛАХ (от учебных задач до олимпиадных задач) Линейные

 

2.22. Вынесите за скобки общий множитель (n натуральное число): 1) x n + 3 + x n - 3) z 3n - z n - 2) y n + 2 - y n - 2, n > 2- 4) 5 n + 4 + 2 5 n + 2-3 5 n + 1. 2.23. Каждому числу поставили в соответствие

 

ЛЕКЦИЯ 15 ПРОСТЫЕ ЧИСЛА Натуральное число p, больше единицы называется простым, если оно делится нацело только на 1 и на себя. Теорема (Эвклид). Множество простых чисел бесконечно. Обозначим через π(x)

 

Тема 3. Элементы алгебраической и аналитической теории чисел Теоретический материал 1. Цепные дроби. Конечной цепной дробью называется выражение a +, (1) где a - целое число, a, i > 0, натуральные числа,

 

Http://vk.ucoz.et/ Операции над многочленами k a k Многочленом (полиномом) степени k называется функция вида a, где переменная, a - числовые коэффициенты (=,.k), и. Любое ненулевое число можно рассматривать

 

Пензенский государственный педагогический университет имени В. Г. Белинского М. В. Глебова В. Ф. Тимербулатова ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО АЛГЕБРЕ МНОГОЧЛЕНОВ Учебно-методическое пособие Пенза Печатается по

 

ДЕЛИМОСТЬ ЦЕЛЫХ ЧИСЕЛ С ОСТАТКОМ Пусть m целое число, а n натуральное число Если m > n и m не делится на n нацело, то возможно деление m на n с остатком Определение 3 Для любого целого числа m и любого

 

Авдошин С.М., Савельева А.А. Алгоритм решения систем линейных уравнений в кольцах вычетов Разработан эффективный алгоритм решения систем линейных уравнений в кольцах вычетов , эквивалентный по сложности

 

ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа) I 1 / 88 Часть I Конечные поля (поля Галуа) I ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа) I 2 / 88 Поля вычетов по модулю простого числа

 

5 Алгебраические структуры 6 Определение Бинарная операция на множестве S есть отображение S S в S То есть, является правилом, которое каждой упорядоченной паре элементов из S ставит в соответствие некоторый

 

/Е Э лементы теории чисел и. рочев 28 августа 2018 г. Оглавление Оглавление i 1 Целые числа 1 1.1 Вводные задачи....................................... 1 1.2 Наибольший общий делитель..............................

 

Глава Целые, рациональные и действительные числа. Деление с остатком. Каждое из чисел ±23, ±4 разделите с остатком на каждое из чисел ±5. 2. Найдите все положительные делители числа 42. 3. Сейчас 3 часов.

 

Дифференциальные уравнения лекция 4 Уравнения в полных дифференциалах. Интегрирующий множитель Лектор Шерстнёва Анна Игоревна 9. Уравнения в полных дифференциалах Уравнение d + d = 14 называется уравнением

 

Тема. Основы элементарной теории чисел и приложения-. Первообразные корни, индексы. Теоретический материал Пусть а, m натуральные взаимно простые числа, причем m, тогда, согласно теореме Эйлера, a m)

 

Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Теория пределов Составитель: доцент

 

Раздел 2. Теоретико-численные методы в криптографии Задание на самостоятельную работу Изучить алгоритмы, которые широко применяются в криптографии. Элементы теории чисел: расширенный алгоритм Евклида-

 

Тематический план составлен на основе программного материала 206-207 уч.года по учебнику «Алгебра 8» под ред. А.Г.Мордковича с учетом рекомендованного обязательного минимума содержания образования Тема

 

Лекция 2. Свойства биномиальных коэффициентов. Подсчет сумм и метод производящих функций (конечный случай). Полиномиальные коэффициенты. Оценки биномиальных и полиномиальных коэффициентов. Оценки сумм
На кружке показала, как в столбик можно извлекать квадратные корни. Вычислить корень можно с произвольной точностью, найти сколько угодно цифр в его десятичной записи, даже если он получается иррациональным. Алгоритм запомнился, а вопросы остались. Непонятно было, откуда взялся метод и почему он дает верный результат. В книжках этого не было, а может, просто не в тех книжках искала. В итоге, как и многое из того, что на сегодняшний день знаю и умею, вывела сама. Делюсь своим знанием здесь. Кстати сказать, до сих пор не знаю, где приведено обоснование алгоритма)))
Итак, сначала на примере рассказываю, “как работает система”, а потом объясняю, почему она на самом деле работает.
Возьмем число (число взято “с потолка”, только что в голову пришло).
1. Разбиваем его цифры на пары: те, что стоят слева от десятичной запятой, группируем по две справа налево, а те, что правее – по две слева направо. Получаем .
2. Извлекаем квадратный корень из первой группы цифр слева — в нашем случае это (ясно, что точно корень может не извлекаться, берем число, квадрат которого максимально близок к нашему числу, образованному первой группой цифр, но не превосходит его). В нашем случае это будет число . Записываем в ответ — это старшая цифра корня.
3. Возводим число, которое стоит уже в ответе — это — в квадрат и вычитаем из первой слева группы цифр — из числа . В нашем случае остается .
4. Приписываем справа следующую группу из двух цифр: . Число , которое уже стоит в ответе, умножаем на , получаем .
5. Теперь следите внимательно. Нам нужно к числу справа приписать одну цифру , и число умножить на , то есть на ту же самую приписанную цифру. Результат должен быть как можно ближе к , но опять-таки не больше этого числа. В нашем случае это будет цифра , ее записываем в ответ рядом с , справа. Это следующая цифра в десятичной записи нашего квадратного корня.
6. Из вычитаем произведение , получаем .
7. Далее повторяем знакомые операции: приписываем к справа следующую группу цифр , умножаем на , к полученному числу > приписываем справа одну цифру, такую, чтобы при умножении на нее получилось число, меньшее , но наиболее близкое к нему –– это цифра –– следующая цифра в десятичной записи корня.
Вычисления запишутся следующим образом:

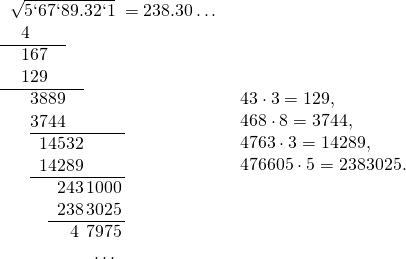
А теперь обещанное объяснение. Алгоритм основан на формуле

Комментариев: 51

1. 2 Антон:

   Слишком сумбурно и запутано. Разложите всё по пунктам и пронумеруйте их. Плюс: объясните откуда в каждом действии мы подставляем нужные значения. Никогда раньше не вычислял корень в столбик – разобрался с трудом.

2. 5 Юлия:

3. 6 :

   Юлия, 23 на данный момент записано справа, это две первые (слева) уже полученные цифры корня, стоящие в ответе. Умножаем на 2 согласно алгоритму. Повторяем действия, описанные в пункте 4.

4. 7 zzz:

   ошибка в “6. Из 167 вычитаем произведение 43 * 3 = 123 (129 нада), получаем 38.”
   непонятно как после запятой получилось 08…

5. 9 Федотов Александр:

   А ещё в докалькуляторную эпоху нас в школе учили не только квадратный, но и кубический корень в столбик извлекать, но это более нудная и кропотливая работа. Проще было таблицами Брадиса воспользоваться или логарифмической линейкой, которую мы уже в старших классах изучали.

6. 10 :

   Александр, Вы правы, можно извлекать в столбик и корни больших степеней. Я собираюсь написать как раз о том, как находить кубический корень.

7. 12 Сергей Валентинович:

   Уважаемая Елизавета Александровна! Мной в конце 70-х разработана схема автоматического (т.е. не подбором) вычисления квадр. корня на арифмометре “Феликс”. Если заинтересуетесь, могу выслать описание.

8. 14 Vlad aus Engelsstadt:

   (((Извлечение квадратного корня в столбик)))
   Алгоритм упрощается, если использовать 2-ную систему счисления, которую изучают в информатике, но полезно и в математике. А.Н. Колмогоров в популярных лекциях для школьников приводил этот алгоритм. Его статью можно найти в “Чебышёвском сборнике” (Математический журнал, ищите ссылку на него в интернете)
   К случаю сказать:
   Г.Лейбниц в свое время носился с идеей о переходе от 10-ной системы счисления к двоичной из-за ее простоты и доступности для начинающих (младших школьников). Но устоявшиеся традиции ломать это все равно что лбом ломать крепостные ворота: можно, но бесполезно. Вот и получается как по наиболее цитируемому в былые времена бородатому философу: традиции всех мертвых поколений подавляют сознание живых.
   До следующих встреч.

9. 15 Vlad aus Engelsstadt:

   ))Сергей Валентинович, да, мне интересно…((
   Бьюсь об заклад, что это вариация под “Феликс” Вавилонского метода извлечения коня квадратного методом последовательных приближений. Этот алгоритм был перекрыт методом Ньютона (метод касательных)
   Интересно, не ошибся ли я в прогнозе?

10. 18 :

    2Vlad aus Engelsstadt
    Да, алгоритм в двоичной системе должен быть проще, это довольно очевидно.
    О методе Ньютона. Может, оно и так, но все равно интересно

11. 20 Кирилл:

    Спасибо большое. А алгоритма так и нету, неизвестно откуда он взялся, но результат правильный получается. СПАСИБО БОЛЬШОЕ! Долго искал это)

12. 21 Александр:

    А каким образом пойдёт извлечение корня из числа, где вторая слева-направо группа весьма мала? к примеру, любимое всеми число 4 398 046 511 104 . после первого вычитания не получается продолжить всё по алгоритму. Объясните пожалуйста.

13. 22 Алексей:

    Да, знаю этот способ. Я, помню, вычитал его в книге “Алгебра” какого-то старого издания. Тогда еще по аналогии сам вывел, как так же в столбик извлекать кубический корень. Но там уже сложнее: каждая цифра определяется уже не в одно (как для квадратного), а в два вычитания, да еще там каждый раз надо перемножать длинные числа.

14. 23 Артем:

    В примере извлечения квадратного корня в столбик из 56789,321 имеются опечатки. Группа цифр 32 приписана дважды к числам 145 и 243, в числе 2388025 вторую 8 необходимо заменить на 3. Тогда последнее вычитание следует записать так: 2431000 – 2383025 = 47975.
    Дополнительно, при делении остатка на увеличенное в два раза значение ответа (без учета запятой), получим добавочное количество значащих цифр (47975/(2*238305) = 0.100658819…), которые следует дописать к ответу (√56789,321 = 238,305… = 238,305100659).

15. 24 Сергей:

    По всей видимости алгоритм пришел из книги Исаака Ньютона “Всеобщая арифметика или книга о арифметических синтезе и анализе”. Вот выдержка из неё:
    ОБ ИЗВЛЕЧЕНИИ КОРНЕЙ
    Чтобы извлечь из числа квадратный корень, прежде всего следует поставить над его цифрами через одну, начиная с единиц, точки. Затем следует в частном или в корне написать цифру, квадрат которой равен или ближайший по недостатку к цифрам или цифре, предшествующим первой точке. После вычитания этого квадрата остальные цифры корня будут последовательно найдены посредством деления остатка на удвоенную величину уже извлеченной части корня и вычитания всякий раз из остатка квадрата последней найденной цифры и ее удесятеренного произведения на названный делитель.

16. 25 Сергей:

    Поправьте ещё название книги “Всеобщая арифметика или книга оБ арифметических синтезе и анализе”

17. 26 Александр:

    Спасибо за интересный материал. Но мне этот метод представляется несколько более сложным, чем нужно, например, школьнику. Я применяю более просто метод, основанный на разложении квадратичной функции с помощью первых двух производных. Формула его такая:
    sqrt(x)= A1+A2-A3, где
    А1 – целое число, квадрат которого ближе всего к х-
    А2 – дробь, в числителе х-А1, в знаменателе 2*А1.
    Для большинства чисел, встречающихся в школьном курсе, этого достаточно, чтобы получить результат с точностью до сотых.
    Если нужен более точный результат, берем
    А3 – дробь, в числителе А2 в квадрате, в знаменателе 2*А1+1.
    Конечно, для применения нужна таблица квадратов целых чисел, но это в школе не проблема. Запомнить эту формулу достаточно просто.
    Меня, правда, смущает, что А3 я получил опытным путем в результате экспериментов с электронной таблицей и не вполне понимаю, почему этот член имеет такой вид. Может, подскажете?

18. 27 Александр:

    Да, я тоже рассматривал эти соображения, но дьявол кроется в деталях. Вы пишете:
    “поскольку a2 и b отличаются уже довольно мало”. Вопрос именно стоит, насколько мало.
    Эта формула хорошо работает на числах второго десятка и гораздо хуже (не до сотых, только до десятых) на числах первого десятка. Почему так происходит уже трудно понять без привлечения производных.

19. 28 Александр:

    Я уточню, в чем я вижу преимущество предложенной мной формулы. Она не требует не вполне естественного разбиения чисел на пары цифр, которое, как показывает опыт, часто выполняется с ошибками. Смысл ее очевиден, а для человека, знакомого с анализом, тривиален. Хорошо работает на числах от 100 до 1000, наиболее часто встречающихся в школе.

20. 29 Александр:

    Кстати, я немного покопался и нашел точное выражение для А3 в моей формуле:
    А3= А22 /2(A1+A2)

21. 30 vasil stryzhak:

    В наше время, повсеместного использования вычислительной техники, вопрос извлечения квадратного коня из числа с практической точки зрения не стоит. Но для любителей математики, несомненно, представляют интерес различные варианты решения данной задачи. В школьной программе способ данного вычисления без привлечения дополнительных средств должен иметь место наравне с умножением и делением в столбик. Алгоритм вычисления должен быть не только запоминаемым, но и понятным. Классический метод, предоставленный в данном материале для обсуждения с раскрытием сущности, в полной мере соответствует вышеназванным критериям.
    Существенным недостатком предлагаемого Александром способа является использование таблицы квадратов целых чисел. Каким большинством чисел встречающихся в школьном курсе она ограничена автор умалчивает. Что касается формулы, то в целом она мне импонирует в виду относительно высокой точностью вычисления.

22. 31 Александр:

    для 30 vasil stryzhak
    Я ни о чем не умолчал. Таблица квадратов предполагается до 1000. В мое время в школе ее просто заучивали наизусть и она была во всех учебниках математики. Я в явном виде назвал этот интервал.
    Что до вычислительной техники, то она не применяется, в основном, на уроках математики, если только не идет специально тема применения калькулятора. Калькуляторы сейчас встроены в устройства, запрещенные к применению на ЕГЭ.

23. 32 vasil stryzhak:

    Александр, спасибо за разъяснение!Я считал,что для предлагаемого метода теоретически необходимо помнить или пользоваться таблицей квадратов всех двузначных чисел.Тогда для подкоренных чисел не входящих в интервал от 100 до 10000 можно использовать прием их увеличения или уменьшения на необходимое количество порядков переносом запятой.

24. 33 vasil stryzhak:

25. 39 АЛЕКСАНДР:

    МОЯ ПЕРВАЯ ПРОГРАММА НА ЯЗЫКЕ “ЯМБ” НА СОВЕТСКОЙ МАШИНЕ “ИСКРА 555″ БЫЛА НАПИСАНА ДЛЯ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА ПО АЛГОРИТМУ ИЗВЛЕЧЕНИЯ В СТОЛБИК! а сейчас забыл как извлекать в ручную!

В предисловии к своему первому изданию “Вцарстве смекалки” (1908 год) Е. И. Игнатьев пишет:“... умственную самодеятельность,сообразительность и “смекалку” нельзя ни“вдолбить”, ни “вложить” ни в чью голову.Результаты надёжны лишь тогда, когда введение вобласть математических знаний совершается влёгкой и приятной форме, на предметах и примерахобыденной и повседневной обстановки,подобранных с надлежащим остроумием изанимательностью”.
В предисловии к изданию 1911 г “Роль памяти вматематике” Е.И. Игнатьев пишет “… в математикеследует помнить не формулы, а процесс мышления”.
Для извлечения квадратного корня существуюттаблицы квадратов для двухзначных чисел, можноразложить число на простые множители и извлечьквадратный корень из произведения. Таблицыквадратов бывает недостаточно, извлечение корняразложением на множители - трудоёмкая задача,которая тоже не всегда приводит к желаемомурезультату. Попробуйте извлечь квадратныйкорень из числа 209764? Разложение на простыемножители дает произведение 2*2*52441. Методом проб иошибок, подбором – это, конечно, можно сделать,если быть уверенным в том, что это целое число.Способ, который я хочу предложить, позволяетизвлечь квадратный корень в любом случае.
Когда-то в институте (Пермский государственныйпедагогический институт) нас познакомили с этимспособом, о котором сейчас хочу рассказать.Никогда не задумывалась, есть ли у этого способадоказательство, поэтому сейчас пришлосьнекоторые доказательства выводить самой.
Основой этого способа, является состав числа =.
=&, т.е. & 2 =596334.
1. Разбиваем число (5963364) на пары справа налево(5`96`33`64)
2. Извлекаем квадратный корень из первой слевагруппы ( - число 2). Так мыполучаем первую цифру числа &.
3. Находим квадрат первой цифры (2 2 =4).
4. Находим разность первой группы и квадратапервой цифры (5-4=1).
5.Сносим следующие две цифры (получили число 196).
6. Удваиваем первую, найденную нами цифру,записываем слева за чертой (2*2=4).
7.Теперь необходимо найти вторую цифру числа&: удвоенная первая цифра, найденная нами,становится цифрой десятков числа, при умножениикоторого на число единиц, необходимо получитьчисло меньшее 196 (это цифра 4, 44*4=176). 4 - вторая цифрачисла &.
8. Находим разность (196-176=20).
9. Сносим следующую группу (получаем число 2033).
10. Удваиваем число 24, получаем 48.
11.48 десятков в числе, при умножении которого начисло единиц, мы должны получить число меньшее 2033(484*4=1936). Найденная нами цифра единиц (4) и естьтретья цифра числа &.

Доказательство приведено мной для случаев:
1. Извлечение квадратного корня из трехзначногочисла-
2. Извлечение квадратного корня изчетырехзначного числа.


Приближенные методы извлечения квадратногокорня (без использования калькулятора) .
1.Древние вавилоняне пользовались следующимспособом нахождения приближенного значенияквадратного корня их числа х. Число х онипредставляли в виде суммы а 2 +b, где а 2ближайший к числу х точный квадратнатурального числа а (а 2 ?х), и пользовалисьформулой 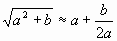. (1)
Извлечем с помощью формулы (1) кореньквадратный, например из числа 28:

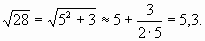
Результат извлечения корня из 28 с помощью МК5,2915026.
Как видим способ вавилонян дает хорошееприближение к точному значению корня.
2. Исаак Ньютон разработал метод извлеченияквадратного корня, который восходил еще к ГеронуАлександрийскому (около 100 г. н.э.). Метод этот(известный как метод Ньютона) заключается вследующем.
Пусть а 1- первое приближение числа (в качестве а 1можно брать значения квадратного корня изнатурального числа - точного квадрата, непревосходящего х) .
Следующее, более точное приближение а 2числанайдетсяпо формуле .

Алгоритм Евклида

Наибольший общий делитель

Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел - это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НОД(12, 18) = 6.
Обозначим исходные данные как М u N. Постановка задачи выглядит следующим образом:
Дано: М, N
Найти: НОД(М, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.

Идея алгоритма Евклида

Идея этого алгоритма основана на том свойстве, что если M>N, то
НОД(М, N) = НОД(М - N, N).
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К - общий делитель М u N (M> N). Это значит, что М = mК, N = nК, где m, n - натуральные числа, причем m > n. Тогда М - N = К(m - n), откуда следует, что К - делитель числа М - N. Значит, все общие делители чисел М и N являются делителями их разности М - N, в том числе и наибольший общий делитель.
Второе очевидное свойство:
НОД(М, М) = М.
Для ручного счета алгоритм Евклида выглядит так:
1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма-
2) заменить большее число разностью большего и меньшего из чисел-
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
Структура алгоритма - цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24.

Шаг	Операция	M	N	Условие
1	ввод М	32
2	ввод N		24
3	M ¹N			32 ¹24, да
4	M>N			32>24, да
5	M:=M-N	8
6	M ¹N			8 ¹24, да
7	M>N			8>24, нет
8	N:=N-M		16
9	M ¹N			8 ¹16, да
10	M>N			8>16, нет
11	N:=N-M		8
12	M ¹N			8 ¹8, нет
13	вывод M	8
14	конец

В итоге получился верный результат.

Программа на АЯ и на Паскале

Запишем алгоритм на АЯ и программу на Паскале.
Вопросы и задания
1. Выполните на компьютере программу Evklid. Протестируйте ее на значениях М= 32, N = 24- М = 696, N = 234.
2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:
НОД(А, B, С) = НОД(НОД(А, В), С).
3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:
А ×В = НОД(А, В) ×НОК(А, В).
Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Алгоритм нахождения НОД делением

1. Большее число делим на меньшее.
2. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
3. Если есть остаток, то большее число заменяем на остаток от деления.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6
a =50b =130whilea !=0andb !=0:ifa >b:a =a % belse:b =b % aprint(a + b)
В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.

Алгоритм нахождения НОД вычитанием

1. Из большего числа вычитаем меньшее.
2. Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
3. Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 - 18 = 12
18 - 12 = 6
12 - 6 = 6
6 - 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6
a =50b =130whilea !=b:ifa >b:a =a - belse:b =b - aprint(a)